Multilevel Deep Reinforcement Learning Framework
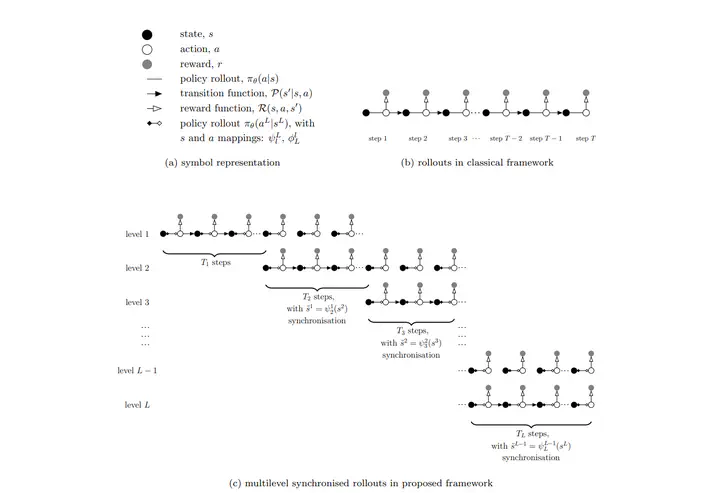 Photo by rawpixel on Unsplash
Photo by rawpixel on UnsplashReinforcement learning (RL) has long been recognized as a promising approach for tackling complex control problems. However, its model-free algorithms often demand a huge amount of data to learn optimal control policies, making them inefficient and computationally intensive.
A significant contributor to this computational burden is the transition function, particularly in cases where model dynamics are described by coupled Partial Differential Equations (PDEs). Here, solving large-scale discretizations of these PDEs adds considerable overhead to RL algorithms, hindering their scalability.
Enter the multilevel RL framework. Inspired by Giles (2015), this approach utilizes sublevel models corresponding to coarser scale discretizations, termed multilevel models. By approximating the objective function of the policy and/or value network using a multilevel Monte Carlo estimate, we can bypass the need for exhaustive Monte Carlo estimates and adapt computational resources to the task’s complexity.
To demonstrate this framework’s effectiveness, I’ve implemented a multilevel version of the proximal policy optimization (PPO) algorithm. In our experiments, the “level” corresponds to the grid fidelity of the simulation-based environment. We’ve explored two case studies featuring stochastic PDEs solved using finite-volume discretization, highlighting the computational savings achieved with multilevel PPO compared to its classical counterpart.
The results are promising, showing significant computational efficiencies that could pave the way for RL to tackle larger and more complex control problems. With multilevel frameworks, we’re poised to overcome the sample inefficiency challenges that have plagued RL, offering a practical pathway towards more efficient and scalable intelligent control systems.

